СОДЕРЖАНИЕ
Математические знаки
| Знак | Значение | Кто ввел | Когда введен |
|---|---|---|---|
| Знаки индивидуальных объектов | |||
| ∞ | бесконечность | Дж. Валлис | 1655 |
| ℮ | основание натуральных логарифмов | Л. Эйлер | 1736 |
| π | отношение длины окружности к диаметру | У. Джонс | 1706 |
| i | корень квадратный из -1 | Л. Эйлер | 1777 |
| i, j, k | единичные векторы | У. Гамильтон | 1853 |
| [i] | целая часть числа, антье | К. Гаусс | 1808 |
| П(α) | угол параллельности | Н.И. Лобачевский | 1835 |
| Знаки переменных объектов | |||
| x, y, z | неизвестные или переменные величины | Р. Декарт | 1637 |
| ¯r | вектор | О. Коши | 1853 |
| а | вектор | О. Хэвисайд | 1891 |
| Знаки индивидуальных операций | |||
| + | сложение | Я. Видман | 1489 |
| − | вычитание | Я. Видман | 1489 |
| × | умножение | У. Оутред | 1631 |
| · | умножение | Г. Лейбниц | 1698 |
| : | деление | У. Джонс Г. Лейбниц |
1633 1684 |
| а2, а3, …аn | степени | Р. Декарт И. Ньютон |
1637 1676 |
| √ | квадратный корень | К. Ридольф Р. Декарт |
1525 1637 |
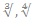 |
корни | И. Ньютон | 1673-83 |
| Log | логарифмы | И. Кеплер | 1624 |
| log | логарифмы | Б. Кавальери | 1632 |
| ln | натуральный логарифм | А. Принсхейм | 1893 |
| sin | синус | Л. Эйлер | 1748 |
| cos | косинус | Л. Эйлер | 1748 |
| tg | тангенс | Л. Эйлер | 1753 |
| arcsin | арксинус | Ж. Лагранж | 1772 |
| Sh | гиперболический синус | В. Риккати | 1757 |
| Ch | гиперболический косинус | В. Риккати | 1757 |
| dx, d2x, d3x, … | дифференциал | Г. Лейбниц | 1675 |
| ∫ydx | интеграл | Г. Лейбниц | 1675 |
| d/dx | производная | Г. Лейбниц | 1675 |
| f′(x), y′, f′x | производная | Ж. Лагранж | 1770, 1779 |
| Δx | разность, приращение | Л. Эйлер | 1755 |
| δ/δx | частная производная | А. Лежандр | 1786 |
 |
определенный интеграл | Ж. Фурье | 1819-22 |
| ∑ | сумма | Л. Эйлер | 1755 |
| ∏ | произведение | К. Гаусс | 1812 |
| ! | факториал | К. Крамп | 1808 |
| |x| | модуль | К. Вейерштрасс | 1841 |
| ||x|| | норма | Э. Шмидт | 1908 |
| lim | предел | С. Люилье | 1786 |
 |
предел | К. Вейерштрасс У. Гамильтон |
1841-45 1853 |
 |
предел | Дж. Лиисем | 1905 |
| ζ(s) | дзета-функция | Б. Риман | 1857 |
| Г(n+1) | гамма-функция | А. Лежандр | 1814 |
| В(p, q) | бета-функция | Ж. Бине | 1839 |
| Δ | дельта (оператор Лапласа) | Р. Мерфи | 1833 |
| ∇ | набла (оператор Гамильтона) | У. Гамильтон | 1853 |
| Знаки переменных операций | |||
| φx | функция | И. Бернулли | 1718 |
| f(x) | функция | Л. Эйлер | 1734 |
| Знаки индивидуальных отношений | |||
| = | равенство | Р. Рекорд | 1557 |
| ≠ | не равно | ||
| ∼ | подобно | Г. Лейбниц | 1710 |
| ≈ | примерно равно | А. Гюнтер | 1882 |
| > | больше | Т. Гарриот | 1631 |
| < | меньше | Т. Гарриот | 1631 |
| ≤ | меньше или равно (не больше) | ||
| ≥ | больше или равно (не меньше) | ||
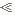 |
мало сравнительно с | ||
 |
велико сравнительно с | ||
| ≡ | тождество | Б. Риман | 1857 |
| || | параллельность | У. Оутред | 1677 |
| ⊥ | перпендикулярность | П. Эригон | 1634 |
 |
равенство и параллельность | ||
| ∩ | пересечение | Дж. Пеано | 1888 |
| ∪ | объединение | Дж. Пеано | 1888 |
| ⊂ | содержится | Э. Шредер | 1890 |
| ⊃ | включается | Э. Шредер | 1890 |
| ∈ | принадлежность | Дж. Пеано | 1895 |
- 2284 просмотра

Добавить комментарий