Электроемкость

 Электроемкость

Два проводника, между которыми имеется электрическое поле, все силовые линии которого начинаются на одном проводнике и заканчиваются на другом, называют конденсатором, а сами проводники – обкладками конденсатора.

В простом конденсаторе величины зарядов на обкладках равны по величине, но противоположны по знаку.

Электроемкость конденсатора равна отношению величины заряда на одной из обкладок к разности потенциалов между ними, т. е.

1)

Электроемкость в системе СИ измеряется в фарадах (Ф). 1 фарада – емкость такого конденсатора, у которого при наличии заряда в 1 Кл (на одной из обкладок) разность потенциалов между обкладками равна 1 В.

Различают по форме проводящих поверхностей плоские, цилиндрические и сферические (шаровые) конденсаторы.

Емкость плоского конденсатора:

2)

где

S	—	величина поверхности одной пластины (меньшей, если они не равны);
d	—	расстояние между пластинами;
ε	—	диэлектрическая проницаемость материала, находящегося между обкладками.

Емкость цилиндрического конденсатора и коаксиального кабеля:

3)

где

b	—	радиус внешнего цилиндра;
a	—	радиус внутреннего цилиндра;
l	—	длина конденсатора.

Емкость сферического конденсатора:

4)

где

a и b

—

радиусы внутренней и внешней сфер.

Емкость двухпроводной линии:

5)

где

d	—	расстояние между осями параллельных проводов;
a	—	их радиус;
l	—	длина.

При параллельном соединении конденсаторов с емкостями C₁, C₂, C₃,…, C_n общая емкость

C1 + C2 + C3 + … + Cn

6)

при последовательном соединении:

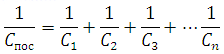7)

Энергия, сосредоточенная в заряженном конденсаторе:

8)

В пространстве, где имеется электрическое поле, сосредоточена энергия. Величина этой энергии объема (плотность энергии) для однородного поля может быть вычислена по формуле

9)

где

E

—

величина напряженности поля.

В случае произвольного поля вводится понятие «плотности энергии в точке»:

Здесь ΔW - энергия, сосредоточенная в объеме ΔV, «стягивающемся» в точку. Если под E понимается напряженность именно в этой точке, то формула (9) оказывается справедливой и для произвольного поля.